Q-Transformer

在机器人领域中，基于监督学习范式的大容量模型往往受限于被提供的高质量数据。之所以产生这种现象是因为人类往往希望机器人能够比专家更专业。同时，也希望机器人能够基于自己收集的数据取得更好的性能，而不是基于演示数据。在以上问题中，强化学习虽然能够展现出卓越的性能，但是基于强化学习算法的大容量模型很难大规模的实例化。本篇论文主要的目的是把大规模多样数据集与基于Transformer的策略架构结合。

原则上，直接替换模型是简单直接的。然而，若要高效的利用大容量模型仍具有很大的挑战。同时，之前基于Tansformer的工作是利用仿真收集数据集，仿真数据没有真实数据更有效。因此，本篇论文主要关注Transformer与离线强化学习的结合。不仅如此，由于Transformer模型主要处理离散数据，因此面对连续动作空间需要离散化，而离散化会造成动作空间指数级爆炸。为了解决该问题，作者提出了per-dimension discretization scheme。同时，为了能够高效的训练，还设计了合适的损失函数，以及Monte-Carlo与n-step returns的混合更新。可见图1所示，Q-Transformer的核心元件。

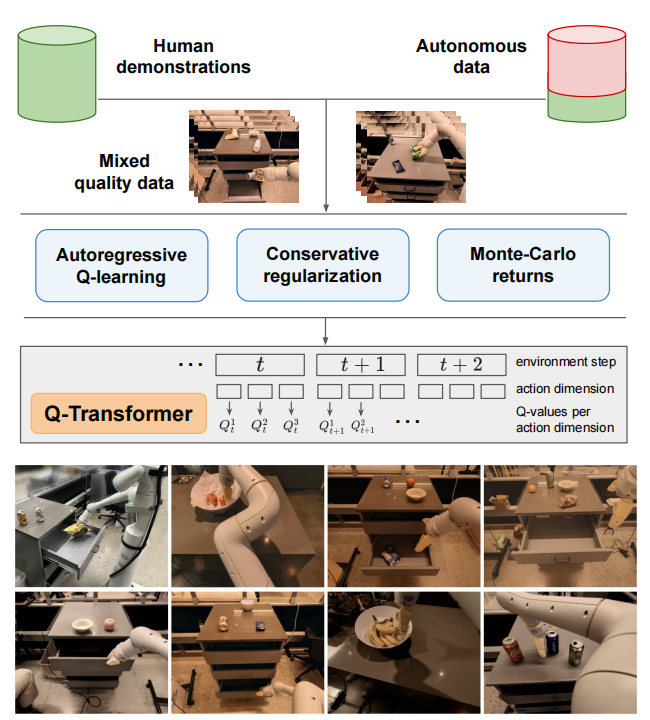
同时，值得一提的是在本论文中作者考虑的是稀疏奖励，其中奖励为$R\in\{0,1\}$的二值奖励。这是因为在机器人操纵领域，这种奖励形式很常见。

自回归离散Q-Learning

在Transformer中加入Q-Learning存在两个挑战，一个是模型的输入必须tokenize，才能使用注意力机制；另一个是必须对离散的动作进行Q值的最大化，同时也要避免维度诅咒。对于动作空间离散化，其背后的思想是把每一维度的动作当作独立的时间步。基于这样的思想，可以离散化单个维度，而不是整个动作空间。

若$\tau=(s_1,a_1,\cdots,s_T,a_T)$表示离线数据集$\mathcal{D}$中长度为$T$的轨迹数据，$a_t$表示时间步为$t$时动作向量，$a_t^i$表示时间步为$t$时第$i$维动作，那么可用以状态$s_{t-w:t}$和动作向量$a_t^{1:i-1}$为条件自回归的$Q$函数定义时间窗口$w$内状态$s_{t-w:t}$下动作$a_t^i$的$Q$值。为了训练$Q$函数，可定义Bellman更新为

$$
Q(s_{t-w:t},a_t^{1:i-1},a_t^i)\leftarrow\begin{cases}
\underset{a^{i+1}_t}{max}Q(s_{t-w:t},a_t^{1:i},a_{t}^{i+1}) & if\quad i\in\{1,\ldots,d_{\mathcal{A}-1}\}\\\\
R(s_t,a_t)+\gamma\underset{a^1_{t+1}}{max}Q(s_{t-w+1:t+1},a_{t+1}^1) & if\quad i=d_{\mathcal{A}}\tag{1.1}
\end{cases}
$$
式(1.1)中$i\in\{1,\ldots,d_{\mathcal{A}}-1\}$，如图(2)所示，$Q$值的更新。具体离散化技术可见：Sequential DQN

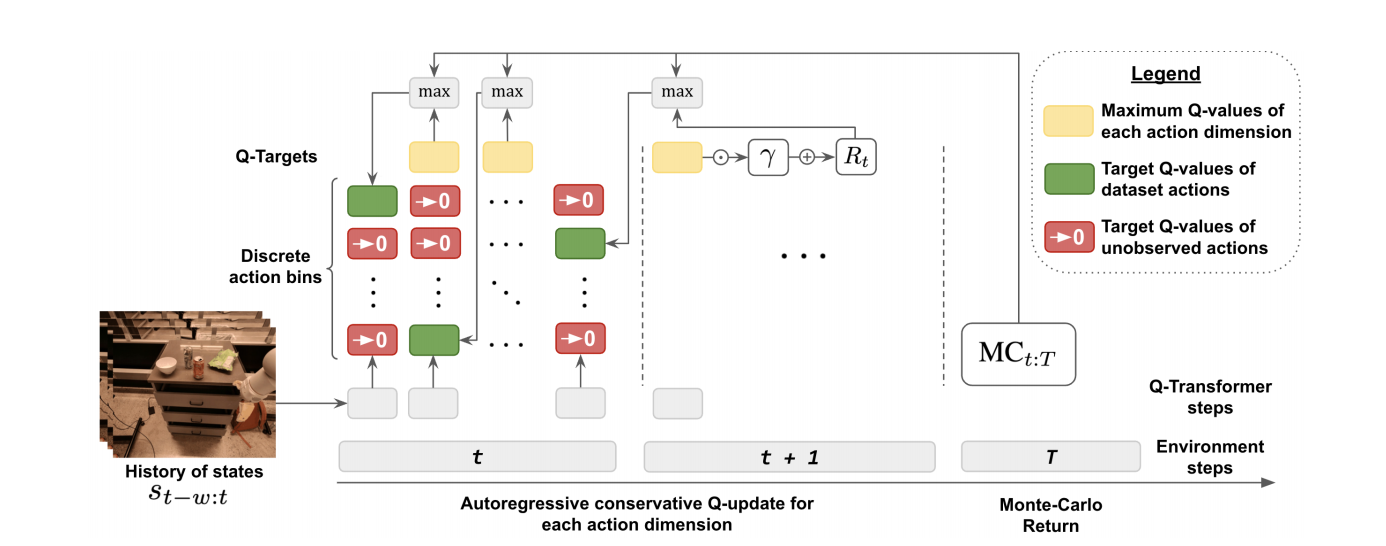
根据文献[1]，可知，式(1.1)的Bellman更新并没有改变Q-Learning算法的优化特性，对于给定的马尔科夫决策过程其Bellman最优仍保持。

保守型Transformer架构的Q-Learning

为了能够利用大量数据训练Transformer，基于离线强化学习算法CQL学习。在CQL算法中为了应对分布偏移造成的高估问题，最小化数据集分布之外的动作。然而，根据文献[3]可知，正则化的Q函数在面对稀疏奖励$R\in\{0,1\}$时会产生负值，即会产生比最小可能累积奖励更小的值。

本文处理该问题的思想是正则化的Q值应尽可能接近最小可获得累积奖励。更确切的说，若用$\mathcal{R}_{min}$表示最小奖励，那么时间窗口数为$T$时，正则化的Q值应接近$\mathcal{R}_{min}\cdot T$，CQL目标函数可变为
$$
J=\frac{1}{2}\underset{(i),TD error}{\underbrace{\mathbb{E}_{s\sim\mathcal{D},a\sim\pi_{\beta}(a\vert s)}[(Q(s,a)-\mathcal{B}^*Q^k(s,a))^2]}}+\alpha\frac{1}{2}\underset{(ii),conservative\quad regularization \mathcal{L}_C}{\underbrace{\mathbb{E}_{s\sim\mathcal{D},a\sim\tilde{\pi}_{\beta}(a\vert s)}[(Q(s,a)-0)^2]}}\tag{1.2}
$$
式(1.2)中，$\tilde{\pi}_{\beta}(a\vert s)=\frac{1}{Z(s)}\cdot(1.0-\pi_{\beta}(a\vert s))$表示数据集分布之外的动作分布。

混合更新

若数据集中包含好的轨迹和次优的轨迹，那么利用Monte-Carlo估计会加速Q-Learning的学习。这是因为MC估计会沿着更好的轨迹产生更快的价值传递。这种现象在文献[4]中已经得到观察。根据这个观测Q-Transformer的目标值设定为$max(MC_{t:T},Q^{targ}(s_t,a_t))$，这种Bellman更新并不会改变模型最终的拟合结果。同时，该目标值背后的思想还有：MC回报与非最优策略的Q函数均为$Q^*(s_t,a_t)$的下界，因此可取最大化。

同时，也注意到关于动作维度的n-step returns明显的提高学习速度。虽然该方式引入了偏差，但是经过剥离研究发现偏差是小的，这些均与文献[5]一致。

值得一提的是，Q-Transformer训练时也利用了文献[6]中Thinking while Moving的思想，从而使Manipulation任务中机器人的不同关节可以异步执行。

接下来，简单讲一下Q-Transformer架构。如图3所示，Q-Transformer架构。

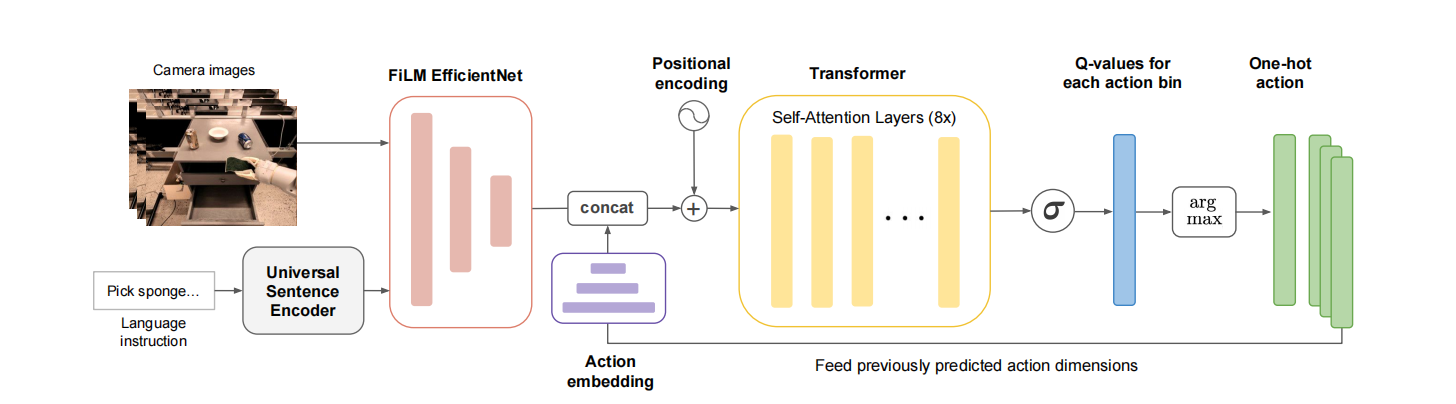
该网络架构由两大部分组成，分别是FiLM或EfficientNet网络和Transformer网络。其中，FiLM或EfficientNet网络用于编码视觉信息与语言信息；Transformer网络的输出经过Sigmoid处理形成动作向量。

参考文献

[1] Chebotar Y, Vuong Q, Hausman K, et al. Q-transformer: Scalable offline reinforcement learning via autoregressive q-functions[C]//Conference on Robot Learning. PMLR, 2023: 3909-3928.

[2] Metz L, Ibarz J, Jaitly N, et al. Discrete sequential prediction of continuous actions for deep rl[J]. arXiv preprint arXiv:1705.05035, 2017.

[3] Kumar A, Singh A, Tian S, et al. A workflow for offline model-free robotic reinforcement learning[J]. arXiv preprint arXiv:2109.10813, 2021.

[4]Wilcox A, Balakrishna A, Dedieu J, et al. Monte carlo augmented actor-critic for sparse reward deep reinforcement learning from suboptimal demonstrations[J]. Advances in Neural Information Processing Systems, 2022, 35: 2254-2267.

[5] Hessel M, Modayil J, Van Hasselt H, et al. Rainbow: Combining improvements in deep reinforcement learning[C]//Proceedings of the AAAI conference on artificial intelligence. 2018, 32(1).

[6] Xiao T, Jang E, Kalashnikov D, et al. Thinking while moving: Deep reinforcement learning with concurrent control[J]. arXiv preprint arXiv:2004.06089, 2020.